Algumas aplicações de funções em outras Áreas..

 Dentre as aplicações encontradas, as mais relevantes foram: lançamento de projéteis, controle de processos (projetos de reatores), faróis de automóveis, , antenas parabólicas e radares, na geometria e nos esportes.

Análise e Controle de Processos: Segundo informações de profissionais da área de engenharia um reator é um equipamento utilizado para produzir reações químicas. Um exemplo muito prático é a panela de pressão no sentido de que propicia reações químicas entre os alimentos nela contidos. Outro exemplo são os reatores do Polo Petroquímico que produzem a matéria-prima para algumas empresas, como de plásticos ou de tintas. Neste sentido, para manter a temperatura de um reator constante, modela-se a situação com uma função quadrática expressa da seguinte forma:  Equação da função de Transferência onde kc é uma constante do processo, obtida através da construção de gráficos experimentais.

Lançamento de Projéteis: Quando se lança um objeto no espaço (pedra, tiro de canhão,...) visando alcançar a maior distância possível, tanto na horizontal como na vertical, a curva descrita pelo objeto é aproximadamente uma parábola, se considerarmos que a resistência do ar não existe ou é pequena. O lançamento de projéteis é modelado por uma função quadrática porque é um movimento acelerado pela ação do campo gravitacional.

 

Queda Livre: Na queda livre dos corpos, o espaço ( s ) percorrido é dado em função do tempo ( t ), por uma função quadrática s(t) = 4,9 t² em que a constante 4,9 é a metade da gravidade que é 9,8 m/s² .

 

Antenas Parabólicas e Radares: Quando um satélite artificial é colocado em uma órbita geoestacionária, ele emite um conjunto de ondas eletromagnéticas que poderão ser captadas pela antena parabólica ou radar, uma vez que o feixe de raios atingirá a antena que tem formato parabólico e então ocorrerá a reflexão desses raios exatamente para um único lugar denominado foco da parábola.

 

Faróis de Automóveis: Se colocarmos uma lâmpada no foco de uma parábola e esta emitir um conjunto de raios luminosos que venham a refletir sobre um espelho parabólico de um farol, os raios refletidos sairão todos paralelamente ao eixo que contém o foco e o vértice da parábola. Esta é uma propriedade geométrica importante lidada à Ótica que permite valorizar bastante o conceito de parábola.

A função exponencial expressa um crescimento ou um decrescimento característico de alguns fenômenos da natureza, bem como o funcionamento dos juros compostos, importantes na matemática financeira.

Vamos explorar um pouco algumas dessas aplicações. 

1) Geralmente, o crescimento de determinados seres vivos microscópicos, como as bactérias, acontece exponencialmente. Dessa forma, é comum o uso de funções exponenciais relacionado a problemas dessa natureza.

Exemplos:

A) (PUC/MG - adaptada) - O número de bactérias em um meio duplica de hora em hora. Se, inicialmente, existem 8 bactérias no meio, ao fim de 10 horas o número de bactérias será:



Resolução:

No tempo t = 0, o número de bactérias é igual a 8.
No tempo t = 1, o número de bactérias é dado por 8.2 = 16.
No tempo t = 2, o número de bactérias é dado por 8.2.2 = 32.
Assim, no tempo t = x, o número de bactérias é dada por  Logo, no tempo desejado, ou seja, ao fim de 10 horas, o número de bactérias será de 
Resposta: E.

B) (UNISA) - Sob certas condições, o número de bactérias B de uma cultura, em função do tempo t, medido em horas, é dado por  Isso significa que 5 dias após a hora zero o número de bactérias é: 


Resolução:

5 dias após o início da hora zero representam um total de 5.24 = 120 horas.
Assim,. Logo, o número de bactérias 5 dias após a hora zero será de 1024.

Resposta: A.

2) A decomposição ou desintegração de determinadas substâncias também acontece segundo um padrão exponencial. A chamada meia vida de uma substância é o tempo necessário para que ela reduza a sua massa pela metade. Eis aqui outro caso de aplicação das funções exponenciais.

Exemplo:

(Vunesp) - Uma certa substância se decompõe aproximadamente segundo a lei  em que K é uma constante, t indica o tempo em minutos e Q(t) indica a quantidade da substância, em gramas, no instante t. Considerando os dados desse processo de decomposição mostrados no gráfico, determine os valores de K e de a.




A FUNÇÃO DE 2º GRAU NA FÍSICA

AA função do 2º grau está presente em inúmeras situações cotidianas, na Física ela possui um papel importante na análise dos movimentos uniformemente variados (MUV), pois em razão da aceleração, os corpos variam a velocidade e o espaço em função do tempo. 

Uma função do 2º grau obedece à seguinte lei de formação f(x) = ax2 + bx + c, 
na Física a expressão que relaciona o espaço em função do tempo é dada pela expressão S = S0 + V0t + (at2)/2, onde 
a: aceleração, S: espaço, V: velocidade e t: tempo. 

Exemplo 1 

Um móvel realiza um MUV obedecendo à função S = 2t2 - 18t + 36, sendo s medido em metros e t em segundos. Em que instante o móvel muda de sentido? 

Resolução: 
A equação do movimento é do segundo grau, então ela descreve uma parábola crescente (a > 0), a mudança de sentido do móvel dará no momento em que ele atingir o ponto mínimo da parábola. Observe a ilustração do movimento do móvel: 



Devemos calcular o ponto mínimo da parábola, dado por: 



Exemplo 2 

Um canhão atira um projétil (figura), descrevendo a função s = -9t2 + 120t, sendo s em metros e t em segundos. Calcule o ponto máximo de altura atingida pelo projétil.



Resolução: 
A função do movimento do projétil descreve uma parábola decrescente (a < 0), o ponto máximo da parábola será a altura máxima atingida pelo projétil. 

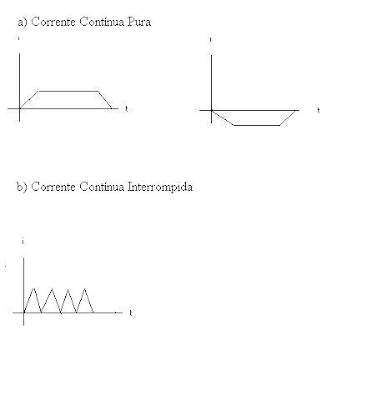
Nas ciências médicas também se utiliza das funções matemáticas para operações na prática. Os gráficos são bastante utilizados, principalmente para demonstrar os batimentos cardíacos e correntes neurológicas. A seguir demonstraremos gráficos de correntes eletroestimuladoras, são correntes elétricas que estimulam o complexo neuromuscular artificialmente, ou seja, são os comandos que o cérebro passa aos músculos.

O gráfico mostra o período de muda ou metamorfose dos artrópodes, que são seres como: a aranha, os besouros, e as minhocas. Estes passam por um processo denominado muda, no qual eles se transformam em seres mais desenvolvidos, algo essencial ao seu crescimento. Neste gráfico observamos que quanto maior o tempo de desenvolvimento (que é o fator X, o termo independente), maior será o tamanho do corpo (que é o fator Y, o termo variável). Então concluímos que tamanho do corpo de um artrópode dependerá do tempo de seu desenvolvimento.

No gráfico acima, que é representado por uma parábola caracterizando uma Função Quadrática, percebemos que Y, é representado pela atividade relativa, ou enzimática, que é o termo variável nessa dada função, entretanto X é representado pelo pH, que é o termo independente. Com isso concluímos que a atividade enzimática depende do pH e quando este estiver entre 7 e 8 alcançaremos o máximo da atividade enzimática aqui representada.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

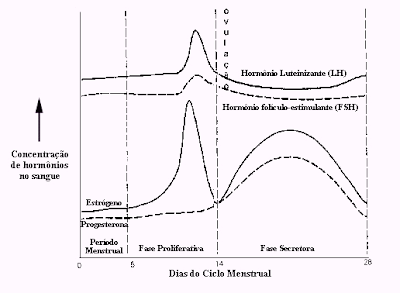
O gráfico acima demonstra o Ciclo Menstrual, no mesmo nota-se os dias e com eles a variação da concentração de hormônios no sangue e quais os tipos. Neste gráfico percebemos que Y é representado pela concentração de hormônios no sangue, porque é o termo variável e que X é representado pelos dias do ciclo menstrual, pois é o termo independente.

 

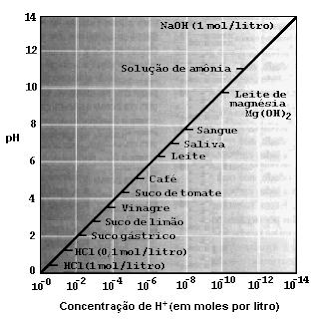
Como percebemos no gráfico acima, demonstra uma Função do 1° grau, pois é representado por uma reta característica da mesma. Nesta função temos o termo Y, que o fator variável, transcrito pelo valor do pH e temos o termo X, que o termo independente, representado pela concentração do cátion de hidrogênio, além disso o gráfico pretende demonstrar o nível de pH e concentração de cátion de hidrogênio em alguns alimentos, em alguns compostos químicos e no sangue. Com este percebemos que quanto maior o pH em algum componente, maior será a concentração de cátion de hidrogênio.